Support Vector Machines (SVMs)

Introduction

Support Vector Machines (SVMs) are a set of supervised learning methods which learn from the dataset and can be used for both regression and classification. An SVM is a kind of large-margin classifier: it is a vector space based machine learning method where the goal is to find a decision boundary between two classes that is maximally far from any point in the training data.

Support Vectors

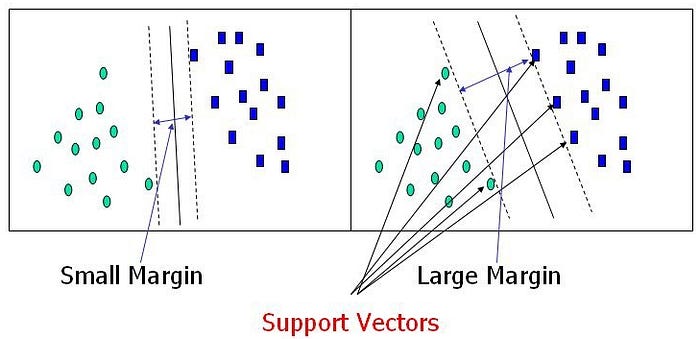
Support Vectors :

The term Support Vectors refers to the co-ordinates of individual observation. Support Vector Machine is a frontier which best segregates the two classes using a hyperplane/ line.

Hyperplane in a line and a plane

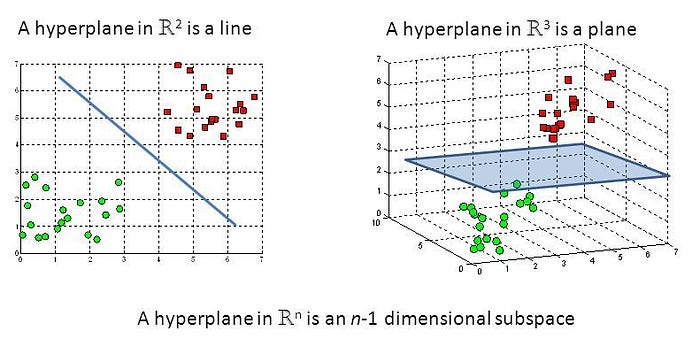
Working of SVM :

An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. New examples are then mapped into that same space and predicted to belong to a category based on which side of the gap they fall.

Identification of a perfect hyperplane. It should be the one that is perfectly segregating two classes.

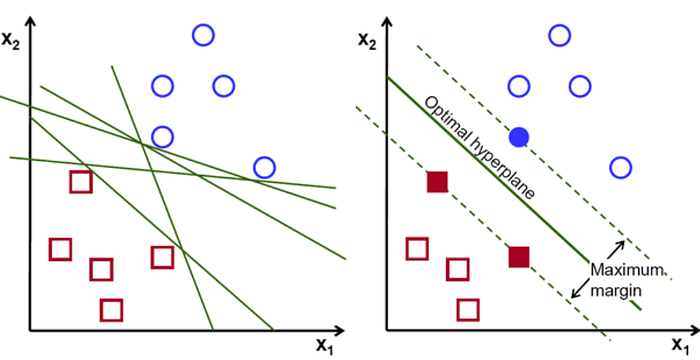
In addition to performing linear classification, SVMs can efficiently perform a non-linear classification using what is called the kernel trick, implicitly mapping their inputs into high-dimensional feature spaces.

Non-Linear Decision Boundary

Kernel Method :

Kernel method is used by SVM to perform a non-linear classification. They take low dimensional input space and convert them into high dimensional input space. It converts non-separable classes into the separable one, it finds out a way to separate the data on the basis of the data labels defined by us.

Performing Non-Linear Classification using Kernel Method

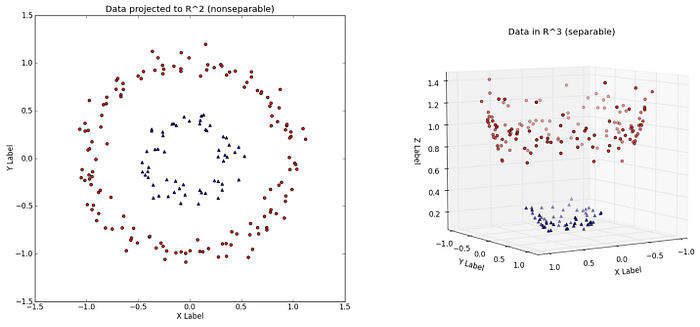
Features and Advantages of SVMs :

1. They maximize the margin of the decision boundary using quadratic optimization techniques which find the optimal hyperplane.
2. It has the ability to handle large feature spaces.
3. SVM’s are very good when we have no idea about our data.
4. Works well with even unstructured and semi-structured data like text, Images and trees.
5. The kernel trick is real strength of SVM. With an appropriate kernel function, we can solve any complex problem.
6. It scales relatively well to high dimensional data.
7. SVM models have generalization in practice, the risk of over-fitting is less in SVM.

Limitations of SVM :

1. It is sensitive to noise.
2. The extension of classification to more than two classes is problematic.
3. Choosing a “good” kernel function is not easy.
4. Long training time for large datasets.
5. Difficult to understand and interpret the final model, variable weights and individual impact.
6. Since the final model is not so easy to see, we can not do small calibrations to the model hence its tough to incorporate our business logic.
7. The SVM hyper parameters are Cost -C and gamma. It is not that easy to fine-tune these hyper-parameters. It is hard to visualize their impact

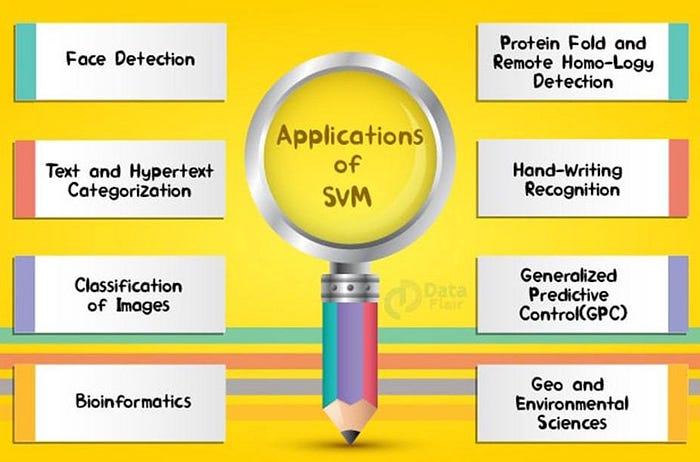
Some applications of SVM :

1. Text (and hypertext) categorization.
2. Image Classification.
3. Bioinformatics (Protein classification, Cancer classification).
4. Hand-written character recognition.
5. Determination of SPAM email.
6. Time Series Analysis.
7. Anomaly Detection.

Applications of SVM