Logistic Regression

Introduction

Logistic Regression is a Supervised learning algorithm widely used for classification. It is used to predict a binary outcome (1/ 0, Yes/ No, True/ False) given a set of independent variables. To represent binary/ categorical outcome, we use dummy variables.

Logistic regression uses an equation as the representation, very much like linear regression. It is not much different from linear regression, except that a Sigmoid function is being fit in the equation of linear regression.

Logistic Regression

Simple Linear and Multiple Linear Regression Equation:

y = b0 + b1x1 + b2x2 + ... + e

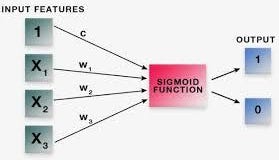
Sigmoid function :

p = 1 / (1 + e ^ -(y))

Logistic Regression Equation :

p = 1 / (1 + e ^ -(b0 + b1x1 + b2x2 +... + e))

where, p is the probability of outcome

y is the predicted output

b0 is the bias or intercept term

Each column in your input data has an associated b coefficient (a constant real value) that must be learned from your training data.

Difference between Linear Regression and Logistic Regression :

• In Linear Regression the target is an continuous (real value) variable while in Logistic Regression the target is a discrete (binary or ordinal) variable.
• The Predicted values in case of Linear Regression are the mean of the target variable at the given values of the input variables. While the Predicted values in Logistic regression are the probability of a particular level(s) of the target variable at the given values of the input variables.

Types of Logistic Regression:

1. Binary Logistic Regression: The target variable has only two 2 possible outcomes. For example, classifying e-mails as Spam or not Spam.
2. Multinomial Logistic Regression: The target variable has three or more categories without ordering. For example, predicting which food is preferred more (Veg, Non-Veg, Vegan)
3. Ordinal Logistic Regression: The target variable has three or more categories with ordering. For example, rating for a movie rating from 1 to 5.

Decision Boundary

To predict which class a data belongs, a threshold can be set. Based upon this threshold, the obtained estimated probability is classified into classes. This threshold is called the Decision Boundary.

Say, if predicted_value ≥ 0.5, then classify email as spam else as not spam. Decision boundary can be linear or non-linear. Polynomial order can be increased to get complex decision boundary.

Decision Boundary in Logistic Regression

Advantages of Linear Regression :

1. It makes no assumptions about distributions of classes in feature space.
2. Easily extended to multiple classes (multinomial regression).
3. Natural probabilistic view of class predictions.
4. Quick to train and very fast at classifying unknown records.
5. Good accuracy for many simple data sets.
6. Resistant to overfitting.

Disadvantages of Logistic Regression :

1. It cannot handle continuous variables.
2. If independent variables are not correlated with the target variable, then Logistic regression does not work.
3. Requires large sample size for stable results.

Logistic Regression Assumptions :

1. Binary logistic regression requires the dependent variable to be binary.
2. Dependent variables are not measured on a ratio scale.
3. Only the meaningful variables should be included.
4. The independent variables should be independent of each other. That is, the model should have little or no multi-collinearity.
5. Logistic regression requires quite large sample sizes.